Вращение большинства механизмов собственных нужд (СН) электростанций и подстанций (ЭС и ПС) осуществляется с помощью электрических приводов, а именно – асинхронными двигателями (АД) с короткозамкнутым ротором, т. к. эти АД считаются самыми распространенными, которые дают возможность пуска от полного напряжения сети без специальных пусковых устройств. Другое преимущество этих АД – восстанавливать нормальный режим работы после глубоких понижений питающего напряжения, которые считаются самозапуском АД [1, 3, 5].
Для механизмов СН ЭС и ПС важно рассчитать токи и напряжение на выводах АД при различных механических нагрузках. Расчет статического режима разветвленной электрической цепи решается методами теории цепей [2, 4] и путем определения расчетного сопротивления АД в цепи. Эти АД в схеме представлены Т-образными или Г-образными схемами замещения [6, 7, 9], которая показана на рис. 1.
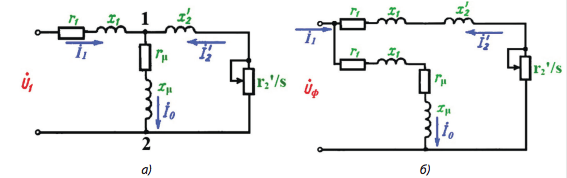
Рис. 1. Схема замещения асинхронного двигателя: а) Т-образная; б) Г-образная
Уравнениям ЭДС и токов соответствует эквивалентная схема замещения, как показано на рис. 1. Таким образом, сложную магнитную цепь АД можно заменить электрической схемой. Сопротивление r’2 /s можно рассматривать как внешнее сопротивление, включенное в обмотку ротора. Оно является единственным переменным параметром схемы. Изменение этого сопротивления эквивалентно изменению нагрузки на валу АД и приводит к изменению s. Тогда не сложно угадать, что скольжение АД в зависимости от нагрузки меняется незначительно (1–6%) [8]. Чем больше мощность АД, тем меньше его s.
Определение эквивалентного сопротивления этих цепей в основном поддерживается необходимостью определения расчетного скольжения АД, которое в простейшем случае представляет собой функцию механической нагрузки (момент сопротивления вращению рабочей машины), амплитуду, частоту и напряжение на обмотке статора [10]. На скольжение могут влиять несимметричность трехфазного напряжения, несинусоидальное напряжение, случайные изменения механической нагрузки [2, 6, 9]. Погрешность определения скольжения 0,001 отн. ед. приводит к значительному увеличению погрешности конечных результатов расчета электрических цепей из-за накопления ошибок в многодвигательном приводе, а также к итерационным расчетам при использовании совместно с методами численных расчетов, при которых накапливается ошибка вычислений.
Для определения скольжения используется уравнение электромагнитного момента электродвигателя и уравнение механической характеристики рабочей машины, приложенной к валу электродвигателя. Известное уравнение электромагнитного момента (механической характеристики) асинхронного двигателя АМ [1, 5, 10] имеет вид:
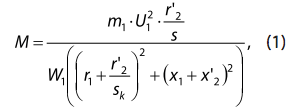
где M – электромагнитный момент;
m1 – количество фаз;
U1 – фазное напряжение на обмотке статора;
s – номинальное скольжение;
sk – критическое скольжение;
W1 – угловая частота вращения магнитного поля;
r1, r'2, x1, x'2 – активное и индуктивное сопротивления утечки обмотки статора и приведенной обмотки ротора соответственно.
Это уравнение отражает процессы в двигателях в рамках традиционных предположений о постоянных значениях параметров r'2, x'2[sub][/sub], без учета насыщения магнитопровода. Это дает существенную погрешность при расчете статических режимов работы электропривода. Особенно остро эта ошибка проявляется в задачах с двигателями, подверженными перегрузкам при изменении напряжения питающей сети, что часто проявляется в сельскохозяйственных электроприводах.
Для расчета электрической цепи с АД аппроксимация экспериментальной механической характеристики АД более удобна, чем уравнение (1). С точки зрения теории приближения, экспериментальная механическая характеристика АД в рабочей зоне должна быть аппроксимирована функцией, дающей погрешность не меньшей величины, чем указанные уравнения.
Наилучшие результаты дает аппроксимирующая функция, где m = a ∙ (1 – e–bs) – электромагнитный момент, а и b – коэффициенты, а е – основание натурального логарифма. Он обеспечивает скорость аппроксимации ξ = 0,0005 для соответствующих значений a и b. Для определения коэффициентов a и b достаточно иметь координаты трех упомянутых выше узлов, что позволяет рассчитать их значения на основе данных каталога AД. Существенно, что эта функция позволяет аналитическое решение вместе с уравнением механической характеристики рабочей машины, заданным традиционным уравнением в виде:
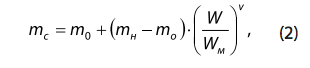
где mс – расчетный момент сопротивления рабочей машины;
m0 – пусковой момент;
mн – момент сопротивления в режиме номинальной нагрузки;
Wм – номинальная угловая частота рабочей машины;
W – номинальная угловая частота расчетная единица;
v – степень, отражающая особенности работающей машины.
Благодаря отмеченным преимуществам, такой вариант аппроксимации механической характеристики становится преимущественным.
Аппроксимация механической характеристики АД с регулируемым напряжением питания имеет лучшую характеристику при использовании следующего уравнения:
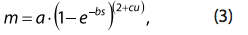
где a, b, s – коэффициенты аппроксимирующей функции;
u – напряжение на АД в относительных единицах (по отношению к номинальному напряжению u = U/Uном).
Необходимо отметить, что значения коэффициентов а и b определяются на основании каталожных данных АД по координатам идеальной скорости режимов работы холостого хода, номинального и критического момента.
После выполнения расчетных операций приведения крутящего момента и скорости к валу АД уравнение (2) принимает вид:
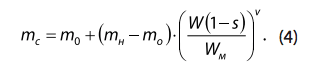
Традиционно для совместного решения уравнений механических характеристик АД и работающей машины используется графоаналитический метод, который плохо приспособлен для использования в математических моделях. В условиях переменных нагрузок и взаимного влияния питающего напряжения многомашинного зала расчеты требуют много времени изза использования циклических расчетов и множественной интерполяции характеристик АД при различных напряжениях питания. Для расчета разветвленной электрической цепи с многомашинными залами требуется минимизировать циклические операции с использованием «прямых» алгоритмов расчета. Относительно совместного решения уравнений (2) и (4) есть такая возможность, как метод возмущений [3, 6, 8, 10].
Совместное решение уравнений (4) и (6) за исключением момента
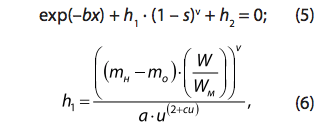
где
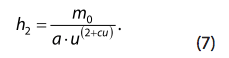
При использовании метода возмущений важно выбрать стратегию решения задачи. Общий смысл решения уравнения этим методом состоит в том, что решение представляется в виде сходящегося ряда. Наиболее часто используется ряд по малому параметру возмущения, описывается следующее:
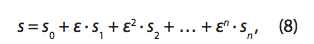
где s0 – корень невозмущенного уравнения, т. е. уравнения, полученного из исходного путем наложения упрощающего условия ε = 0;
s1, s2, …, sn – коэффициенты, не зависящие от ε которые решаются из задачи расчета скольжения.
Правая часть уравнения (8), за исключением s0, представляют собой поправки к корню невозмущенного уравнения, чтобы аппроксимировать корень исходного уравнения (возмущенного).
Наилучшие результаты получаются при использовании параметра возмущения ε = 1, скорректированного в уравнении (7):
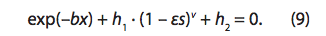
Далее разложим выражение (1 – εs)v в ряд бинома Ньютона и получим [6]:
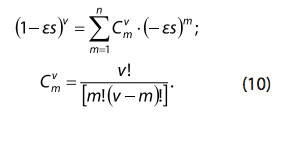
Применение этого метода для расчета электрической цепи показывает, что целесообразно сохранять элементы не выше второго ряда со степенью ε. Остальные элементы ряда не имеют большого значения.
Скольжение имеет большое значение для АД, т. к. скольжение определяет многие свойства АД. Заметно, что при s = 1 ротор АД неподвижен. При уменьшении скольжения частота вращения ротора АД возрастает и при s = 0 ротор АД достигает наибольшей синхронной частоты вращения. Поэтому в этот момент частота вращения магнитного поля статора АД и частота вращения ротора АД считаются одинаковыми.
Поскольку в точках s = –∞; s = 0; s = +∞ момент M = 0 (равен нулю), то между этими точками находятся максимум и минимум момента (рис. 2) [1, 3, 5].
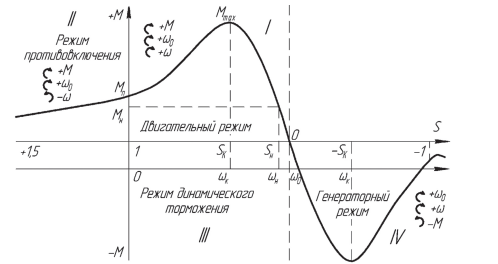
Рис. 2. Графический вид уравнения механической характеристики асинхронного двигателя
Всем известно, что АД, известные как наиболее простые по конструкции и недорогие по производству, обладают основными конкурентными преимуществами в сравнении с другими типами электропривода. Доля АД в системах СН ЭС и ПС занимает порядка 70%. Поэтому всегда нужно осуществлять постоянный контроль за работой асинхронных двигателей и механизмов СН ЭС и ПС с помощью методов идентификации параметров. Учитывая эти факторы, в данной работе исследован простой способ определения скольжения асинхронного двигателя, работающего с нагрузкой, зависящей от параметров электрической цепи.


