Актуальность темы
Математическое моделирование дает большие возможности для изучения экономических взаимосвязей и закономерностей в экономических системах. Использование математического моделирования и ПК дает возможность экспериментировать в экономике [6, 8, 10, 12, 14]. Изменяя условия, можно проанализировать множество вариантов и выбрать наиболее выгодный из них. Методы экономико-математического моделирования актуальны для принятия эффективных управленческих решений в организациях АПК [1, 2, 5, 7, 13].
После того как оптимальное решение задачи найдено, проводится его экономико-математический анализ. Одним из его наиболее важных элементов является изучение того, как влияют на решение изменения различных параметров модели [4, 9, 11]. Например, что произойдет, если спрос на продукцию упадет (возрастет) и, следовательно, придется снизить или повысить цену на то или иное изделие? Изменится ли доходность (значение целевой функции) при изменении запасов и на сколько? Какие ресурсы целесообразно увеличить в первую очередь? К какому результату это может привести? Не являются ли запасы некоторых ресурсов избыточными и не лучше ли вместо затрат на их приобретение и хранение пополнить запасы тех ресурсов, которые в наибольшей степени увеличивают доходность и расходуются полностью? Как количественно просчитать (оценить) различные варианты «ресурсного» поведения? Получение ответов на перечисленные вопросы и составляет суть экономико-математического анализа оптимальных решений [3].
Модуль «Поиск решения» в табличном процессоре Microsoft Excel, используемый для решения оптимизационных задач, позволяет получить не только само оптимальное решение, но и информацию относительно ценности каждого ресурса, чувствительности оптимального решения к изменению запасов ресурсов, вариациям коэффициентов целевой функции и оценить вклад каждого из ресурсов в доходность. Эти возможности, предоставляемые пакетом, обычно остаются неиспользованными.
«Поиск решения» – разработка компании Frontline Systems Inc., создавшей несколько версий программы, одна из которых входит в состав стандартной комплектации Microsoft Excel и позволяет решать задачи, содержащие до 200 переменных. В оригинальной англоязычной версии надстройка носит название Solver. Для сложных задач с большим количеством переменных и ограничений (до 1000) существует более мощная версия программы – Premium Solver, обладающая более высоким быстродействием.
Цель работы – изучить двойственные оценки в экономико-математическом анализе оптимальных решений в растениеводстве и животноводстве.
Материал и методика исследований
Рассмотрим, как можно применить отчет по устойчивости из модуля «Поиск решения» для экономического анализа оптимального решения, опираясь на такой инструмент, как двойственные оценки и их свойства, на примере следующей задачи.
Определить рациональное сочетание посевов ржи, пшеницы, гречихи и поголовья коров. Для их возделывания выделяется 900 га пашни, 13 000 чел.-дн. трудовых ресурсов и 1100 ц минеральных удобрений. Объем производства зерна должен быть не менее 18 000 ц, молока – не менее 3220 ц. Критерий оптимальности – максимум товарной продукции.
В табл. 1, составленной на основе раздела «Ограничения» отчета по устойчивости, содержатся необходимые для анализа полученного оптимального решения данные ограничений по ресурсам и по продуктам.
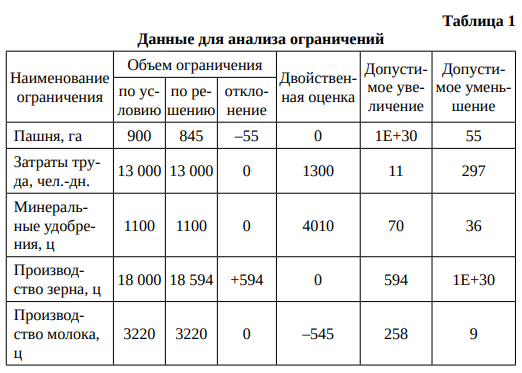
Экономико-математический анализ полученного оптимального решения основывается на двойственных оценках и их свойствах.
Первое свойство двойственных оценок связано с мерой дефицитности ресурсов, продуктов: если ограничение выполняется как строгое равенство, то оценка будет ненулевой, если как неравенство – нулевой. Ненулевая оценка по ресурсу свидетельствует о полном его использовании, дефицитности. В рассматриваемом примере такие ресурсы, как затраты труда и минеральные удобрения, имеют ненулевую оценку, поскольку использованы полностью. Площадь пашни имеет нулевую оценку, поскольку 55 га ее остались неиспользованными.
Для ограничений типа «≥» ненулевая оценка означает, что увеличение объема производства сверх заданного по условию экономически невыгодно, а двойственная оценка показывает степень невыгодности. В рассматриваемом примере ограничение по производству товарного зерна имеет нулевую оценку, следовательно, производство его экономически выгодно: план по производству зерна выполнен полностью, а также получено сверх плана 594 ц. Ограничение по производству молока имеет ненулевую оценку, следовательно, выполнятся как строгое равенство. Для ограничений типа «≥» это означает, что увеличение объема производства сверх заданного по условию экономически не выгодно.
Второе свойство двойственных оценок связано с мерой влияния ограничений на функционал. Нулевые оценки по ресурсам или продуктам свидетельствуют о том, что изменение объема ограничения на единицу не повлияет на значение функционала, т. к. ресурс в оптимальном плане имеется в излишке, а продукт производится сверх плана (в рассматриваемом примере производство зерна).
Ненулевые оценки по ресурсам показывают, насколько увеличится или уменьшится функционал при увеличении или уменьшении ограничения на единицу. В рассматриваемом примере каждый дополнительно привлеченный чел.-дн. трудовых ресурсов будет увеличивать значение целевой функции на 1300 ед., а каждый центнер минеральных удобрений – на 4010 ед.
По продуктам действие оценок противоположное: увеличение ограничения приводит к уменьшению функционала, а уменьшение – к увеличению. В рассматриваемом примере каждый дополнительный центнер товарного молока будет уменьшать значение целевой функции на 545 ед. Такое действие двойственная оценка оказывает в пределах своей устойчивости.
Третье свойство – устойчивость оценок. В линейном программировании под устойчивостью обычно подразумевают неизменность оптимальных решений при изменениях (вариациях) коэффициентов целевой функции, а под чувствительностью – степень влияния правых частей ограничений на прирост либо уменьшение значений целевой функции. Если бы оценки были неустойчивы, т. е. изменялись с изменением каждого параметра задачи, они не представляли бы экономического интереса и потеряли бы свое значение как средство экономико-математического анализа.
Результаты исследований и их обсуждение
В рассматриваемом условном примере сказанное выше будет действительно для изменения ограничений в указанных пределах допустимого увеличения и уменьшения (табл. 1). Так, например, если увеличение запаса минеральных удобрений составит меньше 70 ц, а уменьшение – не более 36 ц, то структура их использования не изменится.
Это же свойство можно применить к значениям переменных величин в оптимальном плане (табл. 2). Так, из трех представленных для примера культур выгодной является пшеница, площадь посева которой составляет 845 га. И она будет оставаться выгодной до тех пор, пока ее целевой коэффициент, равный сейчас 14 300, не уменьшится на величину более 963 ед. Производство озимой ржи будет экономически выгодно, если целевой коэффициент при ней увеличить на значение более 3640 ед., а гречихи – на 700 ед. Двойственная оценка по этим культурам показывает, насколько уменьшится значение целевой функции при введении в план 1 га посева каждой культуры.
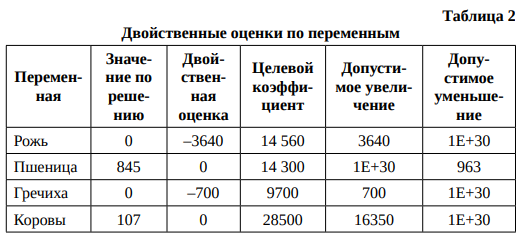
Легко рассчитать, какими для этого должны быть урожайность культур (продуктивность животных), их экономическая оценка в соответствии с принятым критерием оптимальности (в рассматриваемом примере – цены реализации) и диапазон изменения этих показателей, в пределах которого оптимальный план останется неизменным.
Из данных табл. 3 видно, что если урожайность пшеницы будет не менее 20,5 ц (22 – 1,5), а цена реализации – не ниже 606,25 руб. (650 – 43,75), то эта культура останется выгодной. Рассматривать предел допустимого увеличения для нее смысла не имеет.
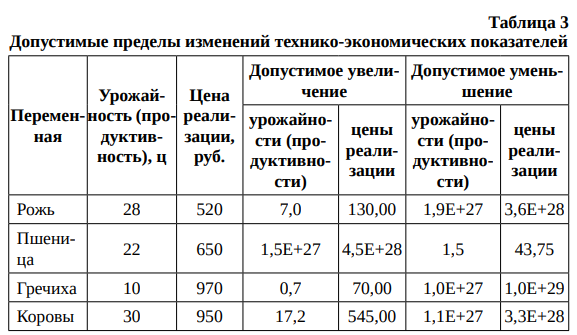
Такие культуры, как рожь и гречиха, не вошли в оптимальное решение. Они имеют отрицательные двойственные оценки, показывающие степень их невыгодности, и аналогичные значения допустимого увеличения, по которым так же, как и по пшенице, можно рассчитать, какими должны быть урожайности и цены реализации этих культур, чтобы они вошли в оптимальный план. Например, если цену реализации гречихи увеличить на 70 руб. или если ее урожайность увеличить на 0,7 ц/га, то выращивание этой культуры станет выгодным. Для того чтобы выращивание ржи было экономически выгодным, нужно ее урожайность увеличить на 7,0 ц/га, а цену реализации – на 130 руб.
Заключение
Таким образом, можно рассчитать колебание цен, а также колебание урожайности сельскохозяйственных культур и продуктивности животных, в пределах которого полученное оптимальное решение будет устойчивым.
Из всего сказанного можно сделать вывод, что отчет по устойчивости, формируемый модулем «Поиск решения» в табличном процессоре Microsoft Excel, является хорошим инструментом для экономического анализа оптимального плана и позволяет заранее оценить результат от внесения в него изменений.


